The molecular structure of silicate melts: how it influences their thermodynamic and rheological pro
- Charles Le Losq
- Mar 20, 2017
- 4 min read
We saw in previous posts that magmas are constituted of a silicate melt, crystals and gas bubbles. At the molecular scale, silicate melts do not present a long-range range order structure, but a disorganised arrangement of different ions that dynamically interact with each others at short and medium range order (from a hundreds of pm to a few nm). From different studies using Nuclear Magnetic Resonance (NMR) and Raman spectroscopy, it is well known that Si and O atoms are arranged in tetrahedral units interconnected between them by their apical oxygen atoms (see figure 1). Such tetrahedral units form the molecular backbone of silicate melts. Alkali (for instance, Na and K) and alkaline-earth (for instance, Ca and Mg) cations do not enter in such tetrahedral units, but break the Si-O-Si bonds and form non-bridging oxygen atoms. As a result of such effect, the melt polymerisation (inter-connection of the tetrahedral units) varies with its content in Si and alkali / alkaline-earth metal cations.
From Silicon-29 Magic Angle Spinning NMR spectroscopy, it is possible to quantify such variations in the structure of the melts, as a function of their composition. Indeed, when rapidly cooled down to room temperature, the melts are quenched into glasses. The glasses Silicon-29 spectra provide information about the environment of the Si atoms in the melts at their glass transition temperature. Silicon-29 signals can be decomposed in several contributions, each linked to Si atoms in tetrahedral units with different numbers of n bridging oxygens (and, hence, 4-n non bridging oxygen; n thus varies between 0 and 4). A denomination allows one to distinguish between the units with different n numbers: the Q^n units (n is an exposant here, but the present blog editor does not allow such refinement...).
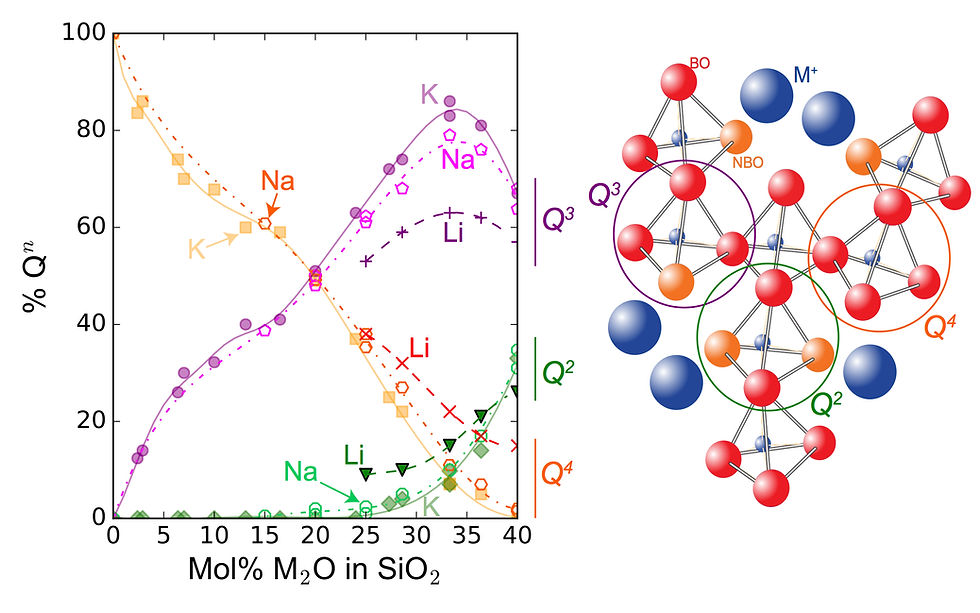
Figure 1: Evolution of the fractions of Q^n units in alkali silicate glasses as a function of their chemical composition. Schematic representations (not at scale) of the tetrahedral units with 2, 3 and 4 bridging oxygens are represented on the right side of the figure. BO and NBO: bridging (Si-O-Si) and non-bridging (Si-O-M) oxygens; M = Li, or Na, or K, an alkali cation. Data are the symbols, lines are fits of the data points with cubic spline functions; see references cited in Le Losq and Neuville (2017) for the source of the Silicon-29 NMR data.
Figure 1 shows how the fractions of different Q^n units varies with the composition of alkali silicate melts. Increasing the alkali content in the melt leads to breakage of Si-O-Si bonds and formation of weak Si-O-M bonds, with M an alkali element. As the melt becomes less depolymerised, the fractions of tetrahedral units containing only bridging oxygens (the Q^4 units) decreases, while those of Q^3 and Q^2 units increases. In a new paper published in Journal of Non-Crystalline Solids, we show that it is possible to assign partial configurational entropies to the different Q^n units present in the structure of the glass. From this, we calculate the melt configurational entropy at its glass transition temperature as well as the energy barriers that inhibits the mobility of Q^n units in the melt structure. Using the Adam and Gibbs (1965) theory of viscous flow, this allows one to calculate the viscosity of silicate melts.
Therefore, in this publication, we show for the first time that it is possible to link our knowledge of the structure of silicate melts to their thermodynamic and rheological properties, in order to produce applicative models that allows one to predict the melt properties. Such model is restrained to the simple Na and K silicate system at the moment, but it clearly emphasises the possibilities offered by such approach for gaining more information about the links between melts/glasses structure and properties. Such approach is critical, as silicate melts represent fundamental materials for Earth sciences, involved in the past formation of the Earth and other silicate planets, such as Mars, as well as in the present Earth geologic activity. Furthermore, silicate glasses are everyday materials used in various technological applications: from glass windows to cellphone covers, with different applications in food containers, car glass windshields, optical fibers critical in the present requirement of fast inter-continental data transmission, or microscopes and telescopes lenses that allows us to study the world from microscopic to galactic scales, or in the glass matrix that help us confining highly hazardous nuclear wastes. Those reasons are why the study of glasses is of fundamental importance, they illustrate why we are studying how the structure and properties of glasses are linked. It allows us to understand the Earth system, to make better glasses (that may also allow to improve the former point!), and to develop innovative applications!
To have further information on the model, check the publication through the link at the end of this page, or email me for the text if you don't have access to JNCS!
Last but not least, we used the open source Julia language to implement the model, which is available for free to reproduce the result of the present publication on my Github account. Further improvements of the model will be pushed in the Github repository, so stay tuned!
Best,
Charles.
Here is the article, click on it to get access through Elsevier:



Comments